Neural networks are seemingly universal learning machines that excel at any task for which we have enough data. In contrast, linear or kernel models, although much more theoretically understood, suffer significantly in cases of model misspecification, which more data cannot alleviate. How are neural networks able to learn structure from data, even if the model is misspecified? At the same time, what is the value of good implicit biases in the architecture of a neural network?

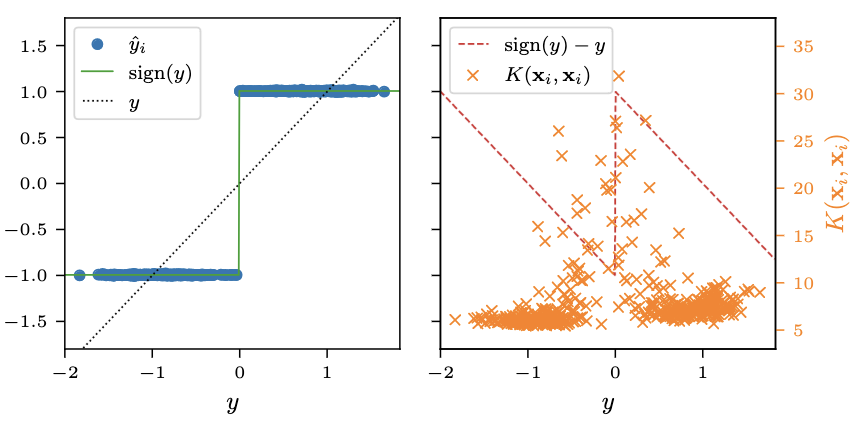
One hypothesis is that the implicit bias of a neural network is captured in the feature space of the neural tangent kernel. However, this kernel only precisely captures the behavior of a neural network in certain unrealistic settings, and actual neural networks have feature spaces which change throughout training, which allows them to better leverage structure in data. In our work, we consider a generic learning setting in which the feature space is allowed to change throughout training and show that this results in structure-inducing regularization of the model. In a neural network context, this corresponds to an approximate low rank penalty on the weight matrices, which explains the success of low rank fine tuning techniques like LoRA.

Sketching or random projections are commonly used tools to reduce computational and memory requirements of data processing algorithms. The idea is that if the random projection is chosen sufficiently, the projection preserves all meaningful structure in the data such that there is no loss in performance. Classically, most guarantees for sketching state that as long as the sketched dimension is roughly as large as the intrinsic dimension of the data, then any algorithm using the sketched data will recover the same solution as if the original unsketched data were used.

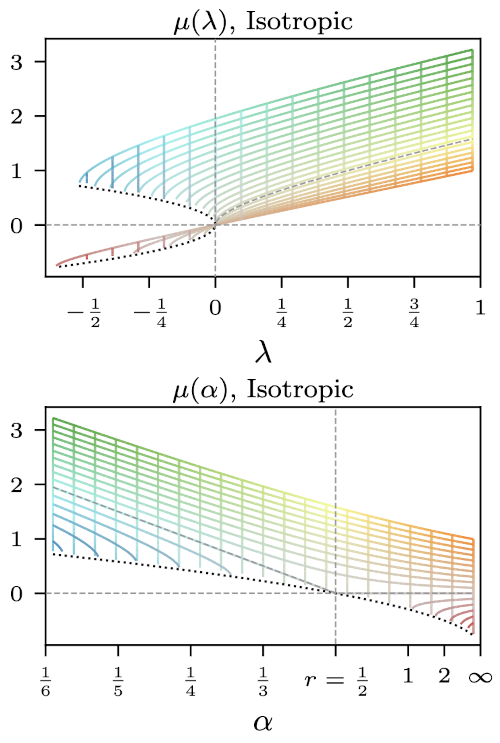
However, in many settings, either the intrinsic dimension is unknown, or other constratings limit us to using smaller dimensions. In this regime, classical results provide no insight into the solutions of sketched algorithms; instead, the resulting solutions are often quite far from the unsketched solution. We consider the particular setting of matrix inversion, as used in least squares (ridge) regression, and using asymptotic random matrix theory, we show that taking the regularized pseudoinverse of a sketched matrix is asymptotically equivalent to taking the inverse of the original matrix at a different regularization level.

This result is not unique to i.i.d. type sketches commonly studied in random matrix theory. In fact, we show that the same type of result holds for any sketch that is free from the data, a notion from free probability theory. Furthermore, the effective regulatization level is a function of the spectral distribution of the sketch itself, and we can characterize effect of the choice of a particular type of sketch.

It is most often the case that we train models on a training dataset from a particular distribution, and then we apply the model in production to data that typically comes from a similar but different distribution. As such, there is an important question that is raised: even if the machine learning task remains the same (that is, the conditional distribution of the labels given data is unchanged), can we rely on in-distribution validation error to reliably perform model selection for models that are applied to out-of-distribution data?

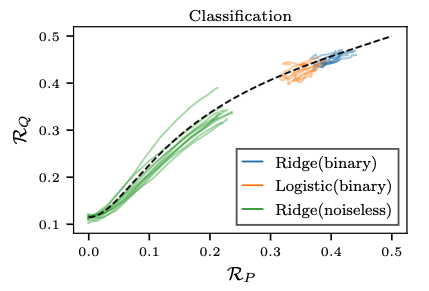
An interesting recent line of empirical work suggests that for "natural" distribution shifts, the answer is affirmative, in the sense that there is a monotonic (often linear) relationship between the in-distribution and out-of-distribution generalization error, for a wide variety of model types and sample sizes. This raises the very interesting theoretical question: when should we expect monotonic risk relations between risks for broad classes of machine learning models?

We answer this question for the general class of linear models fit by empirical risk minimization with convex loss and ridge penalty. Remarkably, given certain necessary and sufficient conditions on covariate shift, there exists a monotonic risk relation that depends in no way on loss function, sample size, or regularization strength, and can thus be considered universal. However, the risk relations do depend critically on the risk metric itself, with squared error and misclassification error having drastically different monotonic relations, and some risk metrics like logistic loss and hinge loss having no monotonic relation at all.

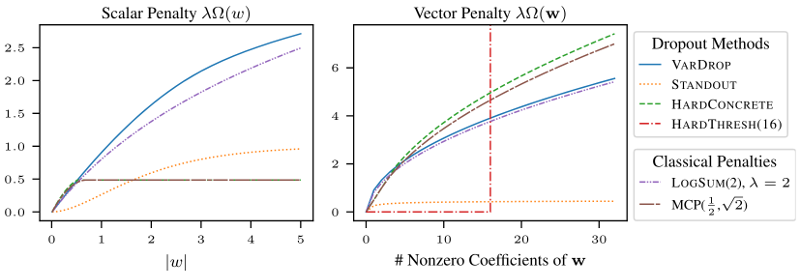
There is a strong connection between ensemble methods and the dropout technique used in deep learning. As we point out, dropout can be viewed as an ensemble where the weights are shared across models. Thus, we can gain some insight into the behavior of ensembles by analyzing dropout, which is much easier to manipulate mathematically. For example, it has been known almost since dropout was proposed that dropout is equivalent to ridge regularization.

The question that this connection helps us to answer is: what happens when we use an adaptive ensemble/dropout algorithm? Interestingly, many state-of-the-art sparsification methods for deep learning can be cast as adaptive dropout algorithms. What's more, we prove a duality between adaptive dropout methods and subquadratic regularization, implying that any adaptive dropout strategy that samples features with higher weights more often results in sparse solutions. Furthermore, these state-of-the-art sparsity methods correspond nearly to sensible classical sparsity-inducing penalty choices.